The TEC drive I have been working on is now mounted as a plug-in card in a 3U 19" rack enclosure like this:
The card next to the TEC drive holds an 80 mm fan which helps cool the heatsinked linear regulators and the linear H-bridge that drives the TEC.
The back of the 19" rack enclosure holds two TRACO POWER PSUs that produce +/-5 V at max 4 A and +/-15 V at max 667 mA. An IEC power-entry module containing the IEC-connector, a fuse, and a power switch is visible far right. Far left is a small PCB for distributing +/-15 V to other cards in the same enclosure.
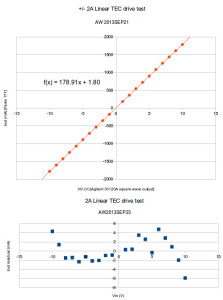
Added cooling allows testing the drive at the max input level of +/-10 V, which should produce (roughly) an output of +/-2 A.
The output current follows 179 mA/V * Vin + 1.8 mA with a maximum nonlinearity of about 6 mA (0.3% of full-scale). Despite the fan-cooling the transistors still get quite hot and staying below 1 A output in continuous operation is probably a good idea.