Category: Programming

PPP comparison with PPP-tools

Here's an example of using PPP-tools to compare PPP solutions from NRCan gpsppp, ESA gLAB, and RTKLIB.

It seems that all programs fix the lat/lon output. However both gLAB and RTKLIB leave the height as a variable parameter. Interestingly it seems there is some peak at the end of the PTBG data and gLAB compensates by raising the height while RTKLIB compensates by raising the clock value.

scipy.stats.chi2.ppf() without scipy

Allantools has a dependence on scipy because it uses scipy.stats.chi2.ppf() (inverse of the chi-squared cumulative distribution function) in the code for confidence intervals.

When testing scipy takes quite a long time to install and the whole package seems a bit overkill for just this one function.

So I tried implementing it using just numpy. It sort of works, but not for corner cases where p is very close to 1.0 or k is a big number. I get for example:

    top = pow(x, s)*math.exp(-x)*pow(x,k)
OverflowError: (34, 'Numerical result out of range')

Maybe there's something trick when numerically evaluating lower_gamma() using the series expansion that I am missing...

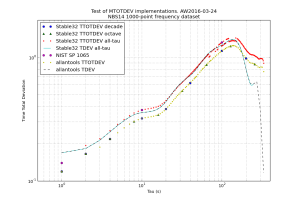
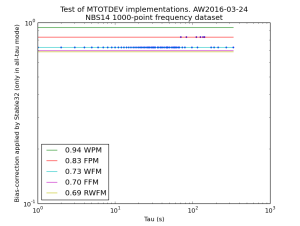
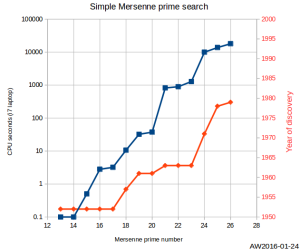
import scipy.stats
import math
import numpy
 
def bisection(function, k, p, a, b, tol):
	# http://code.activestate.com/recipes/578417-bisection-method-in-python/
	assert (function(a,k)-p)*(function(b,k)-p) < 0 # a, b must bracket root
	c = (a+b)/2.0
	while (b-a)/2.0 > tol:
		if (function(c, k)-p) == 0:
			return c
		elif (function(a,k)-p)*(function(c,k)-p) < 0:
			b = c
		else :
			a = c
		c = (a+b)/2.0
	return c
 
def lower_gamma(s,x):
	# lower incomplete gamma function
	# https://en.wikipedia.org/wiki/Incomplete_gamma_function#Evaluation_formulae
	g  = 0
	last_g = 1.0
	done = False
	tol = 1.0e-6
	k=0
	while not done:
		top = pow(x, s)*math.exp(-x)*pow(x,k)
		bot = numpy.prod( [float(s+j) for j in range(k+1) ] )
		dg = float(top)/float(bot)
		if dg == float("Inf"):
			break
		g += dg
		k += 1
		if k>100: # get at least 100 terms in the sum
			if g==0:
				break
			delta = abs(dg/g)
			if delta == float("Inf"):
				break
			if delta < tol:
				done = True
		last_g = g
	return g
 
def chi2_cdf(x, k):
	# chi-squared cumulative density function
	# cdf(x; k) = lower_gamma(k/2, x/2) / gamma(k/2)
	return lower_gamma(k/2.0, x/2.0) / math.gamma(k/2.0)
 
def chi2_ppf(p, k):
	# chi-squared Percent point function (inverse of cdf percentiles).
	# look for x such that
	# p = chi2_cdf( x=chi2_ppf(p, k), k)
	tol = 1e-8
	lolim = 0
	hilim = k
	while (chi2_cdf(lolim,k)-p)*(chi2_cdf(hilim,k)-p) > 0: 
		hilim *= 1.5
	return bisection( chi2_cdf, k, p, lolim, hilim, tol)
 
print "scipy cdf: ",scipy.stats.chi2.cdf(55, 33)	
print "own   cdf: ",chi2_cdf(55, 33)
 
 
print "scipy ppf ", scipy.stats.chi2.ppf(0.4, 33)
print "  own ppf ", chi2_ppf(0.4, 33)
 
# test that we really found the inverse
print scipy.stats.chi2.cdf(scipy.stats.chi2.ppf(0.4, 33), 33)
print chi2_cdf( chi2_ppf(0.4, 33), 33 )
 
# try to check the scipy function against our own function
# for some random input of (p, k)
for n in range(100):
	k = numpy.random.randint(20, 200)
	p = numpy.random.random()
	print k, p,
	a=scipy.stats.chi2.ppf(p, k)
	b=chi2_ppf(p, k)
	ok = numpy.isclose(a, b)
	if ok:
		print  ok
	else:
		print  ok, a, b
	assert ok

Leap second time-stamps for leap-seconds.list

This function generates time-stamps in the format used in leap-seconds.list (on e.g. NTP or PTP servers). The format is integer seconds since 1900-01-01T00:00+00.

import datetime
import pytz
 
 
def generate_ntp_timestamp(year,month,day,hour,minute,second):
    t = datetime.datetime(year,month,day,hour,minute,second,tzinfo=pytz.utc)
    #NTP leap-seconds list wants seconds since 1900
    epoch_start = datetime.datetime(1900,1,1,0,0,0,tzinfo=pytz.utc)
    delta = t-epoch_start
    delta_s = delta.total_seconds()
    return int(delta_s)
 
 
# test that this generates OK values.
# from existing leap-seconds.list
# 2918937600	27	# 1 Jul 1992
# 2950473600	28	# 1 Jul 1993
# 2982009600	29	# 1 Jul 1994
# 3029443200	30	# 1 Jan 1996
# 3076704000	31	# 1 Jul 1997
# 3124137600	32	# 1 Jan 1999
# 3345062400	33	# 1 Jan 2006
# 3439756800	34	# 1 Jan 2009
print "1 Jan 2009: ", generate_ntp_timestamp(2009,1,1,0,0,0)
print "1 Jan 2006: ", generate_ntp_timestamp(2006,1,1,0,0,0)
print "1 Jul 1997: ", generate_ntp_timestamp(1997,7,1,0,0,0)
#output:
#1 Jan 2009:  3439756800
#1 Jan 2006:  3345062400
#1 Jul 1997:  3076704000

Hadamard total deviation in allantools

Following on from modified total deviation mtotdev() the Hadamard total deviation htotdev() algorithm is very similar but instead of phase data takes frequency data. Now included in allantools.

Here's a comarison against Stable32 and the NIST SP 1065 table values.

There's no bias-correction for now, and apparently it is customary not to use htotdev(m=1) at an averaging-factor of 1, but instead use ohdev(m=1). This is why the 'raw' value from allantools at tau=1 in the plot below is a factor of 2 too low.

htotdev_2016-03-27Both mtotdev() and htotdev() are very slow algorithms - help with making them faster would be appreciated!

Sub-second synchronization of cron jobs

cron_syncWe use cron-jobs to control lab instruments once a minute in the lab. I noticed that specifying 'once a minute' to cron produces a start-time for the job with quite a bit of variability. Usually the job starts at 1s past the minute, but sometimes 2s. There's also a random delay of 20 ms to 50 ms (but sometimes up to 300 ms). This probably depends a lot on the hardware. So if we assume the cron-job starts 1s past the minute the worst error I saw in the test above is 1.3 seconds.

Here's a very simple synchronization idea: first ask for a time-stamp, then wait until we are at an inter-second boundary, then continue. This makes the cron-job continue at the inter-second boundary with a maximum error of 6 ms, a fair improvement over 1.3 seconds without any sync code.

import datetime
import time
 
dt1 = datetime.datetime.now() # time-stamp when cron decides to run us
usecs_to_go = 1e6-dt1.microsecond # we want to run at an inter-second boundary
secs_target = 5 # we want to run at 5 seconds past minute
secs_to_go = secs_target - dt1.second -1 # amount of waiting to do.
time.sleep( secs_to_go+ usecs_to_go/1.0e6 )
dt2 = datetime.datetime.now() # now we are synced!?
 
fn = '/home/user/my_cron_log.txt' 
 
# write to logfile for later analysis.
with open(fn,'a+') as f:
    f.write(str(dt1) +" %02d.%06d" % (dt1.second, dt1.microsecond)  + ' run!\n')
    f.write(str(dt2) +" %02d.%06d" % (dt2.second, dt2.microsecond)  + ' sync!\n')
    f.write('\n')

The way to enable this to run from crontab is to add something like this to crontab (use crontab -e):

# m h  dom mon dow   command
  * *  *   *   *     /usr/bin/python /home/user/cron_sync.py

Where cron_sync.py is the name of the script above.

I'd be interested in hearing how this works on other hardware, or if there are some alternative solutions.

Modified Total Deviation in allantools

I wrote a first rough (and very slow!) implementation of Modified Total Deviation mtotdev() for allantools.

mtotdev() combines the features of modified Allan deviation mdev() (being able to distinguish between white and flicker phase modulation) and Total deviation totdev() (better confidence intervals at large tau).

Here are some results. The Time Total Deviation ttotdev() follows trivially from this work also, since it is only a scaled version of mtotdev(). I used the "NBS14" 1000-point frequency dataset and compared my results against Stable32 and those in NIST SP 1065 (Table 31, page 108).

mtotdev_comparison_AW2016-03-24

ttotdev_comparison_AW2016-03-24

The figures show mtotdev() and ttotdev() from Stable32 runs and allantools. I've also added mdev() and tdev() traces to compare against. At first sight this looks strange, but mtotdev() is a biased estimator, and Stable32 applies a bias correction which explains the results.

Somewhat surprisingly Stable32 applies a bias-correction only when run in the "all-tau" mode. These numbers agree with those from the NIST SP 1065 table. For this dataset Stable32 is undecided on what power-law the dataset follows at large tau, which results in deviations that jump up and down (because a different bias-correction is applied at different tau, red datapoints).

When Stable32 is run in "octave-tau" or "decade-tau" mode no bias correction is applied. These numbers agree with the ones from allantools.mtotdev().

mtotdev_bias_AW2016-03-24

This figure shows the ratio of variances between allantools.mtotdev() (no bias correction) and a Stable32 all-tau run (bias correction applied). The lines correspond to the bias-correction values for different noise processes.

There also seems to be a misprint in NIST SP 1065 equation (28) page 26, where it says ttotdev() is scaled by tau-cubed (when tau-squared is correct). Who reads these things anyway - not many it seems 😉

Simple Mersenne prime search

For fun I tried to search for Mersenne primes with a very simple code (below). It finds the 20 first Mersenne primes (all known by 1961) in under a minute. After that it slows down quite a lot and finds the 26th prime (discovered in 1979) in about 5 hours.

mersenne_primes

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

import time
import math
 
# http://stackoverflow.com/questions/16004407/a-fast-prime-number-sieve-in-python
def prime_sieve(n):
    size = n//2
    sieve = [1]*size
    limit = int(n**0.5)
    for i in range(1,limit):
        if sieve[i]:
            val = 2*i+1
            tmp = ((size-1) - i)//val 
            sieve[i+val::val] = [0]*tmp
    return [2] + [i*2+1 for i, v in enumerate(sieve) if v and i>0]
 
# https://en.wikipedia.org/wiki/Trial_division
def trial_division(n):
    """Return a list of the prime factors for a natural number."""
    if n < 2:
        return []
    prime_factors = []
    for p in prime_sieve(int(n**0.5) + 1):
        if p*p > n: break
        while n % p == 0:
            prime_factors.append(p)
            n //= p
    if n > 1:
        prime_factors.append(n)
    return prime_factors
 
def is_prime_trial_division(n):
    return len(trial_division(n)) == 1
 
# https://en.wikipedia.org/wiki/Lucas%E2%80%93Lehmer_primality_test
def is_prime_lucas_lehmer(p):
    s = 4
    M = pow(2,p) -1
    for n in range(p-2):
        s = (pow(s,2)-2) % M
    return s==0
 
n=2 
t0 = time.time()
print "#\tp\ttime\tyear"
log_max_p=15
for p in range(1,pow(2,log_max_p)):
    if is_prime_trial_division(p):
        if is_prime_lucas_lehmer(p):
            elapsed = time.time() - t0
            print "%4d\t%4d\t%.1f s" % (n, p, elapsed)
            n=n+1

NTP Timestamp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

import datetime
import pytz
 
 
def generate_ntp_timestamp(year,month,day,hour,minute,second):
    t = datetime.datetime(year,month,day,hour,minute,second,tzinfo=pytz.utc)
    #NTP leap-seconds list wants seconds since 1900
    epoch_start = datetime.datetime(1900,1,1,0,0,0,tzinfo=pytz.utc)
    delta = t-epoch_start
    delta_s = delta.total_seconds()
    return int(delta_s)
 
 
# test that this generates OK values.
# from existing leap-seconds.list
# 2918937600    27    # 1 Jul 1992
# 2950473600    28    # 1 Jul 1993
# 2982009600    29    # 1 Jul 1994
# 3029443200    30    # 1 Jan 1996
# 3076704000    31    # 1 Jul 1997
# 3124137600    32    # 1 Jan 1999
# 3345062400    33    # 1 Jan 2006
# 3439756800    34    # 1 Jan 2009
print "1 Jan 2009: ", generate_ntp_timestamp(2009,1,1,0,0,0)
print "1 Jan 2006: ", generate_ntp_timestamp(2006,1,1,0,0,0)
print "1 Jul 1997: ", generate_ntp_timestamp(1997,7,1,0,0,0)