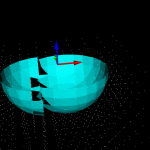
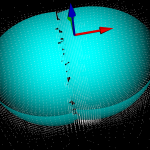
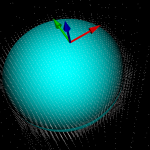
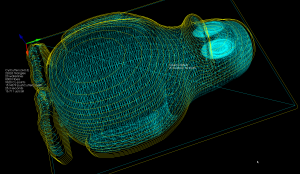
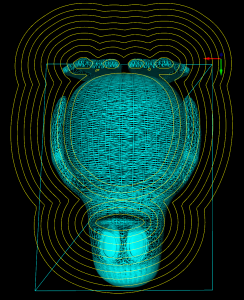
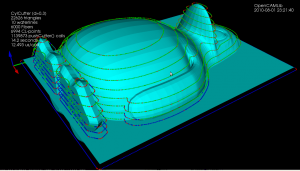
This is my second attempt at a machining simulation where a moving milling tool cuts away voxels from the stock material. To save space an octree data structure is used to store the voxels, and to produce a nice looking surface you store the signed distance to the exact surface in each vertex of the octree. You then use marching-cubes to extract triangles for a distance=0 isosurface in order to draw the stock.
Unlike my first attempt, this works well enough to warrant further experiments (on the to-do list are: differently shaped tools, colouring triangles based on which tool cut the voxel, lathe operations, material removal-rate, etc.). It should be straightforward to hook this up to the EMC2 G-code interpreter so that any G-code, not just densely sampled CL-points from OCL, can be simulated. You could also flip the sign of all the numbers, and simulate an additive process, like 3D printing (reprap / makerbot).
This approach to machining simulation is described in a 2005 paper by Yau, Tsou, and Tong.