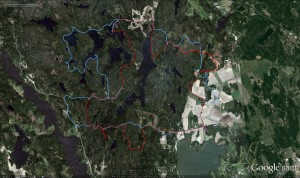
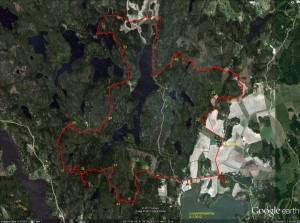
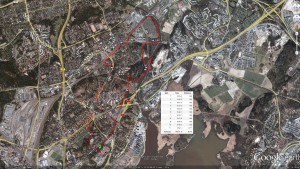
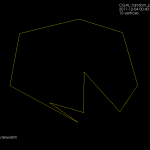
Took part in an 8h rogaining event yesterday. Very wet in the forest with a lot of fallen trees due to the storms over the last few weeks.
We planned a ca. 20km long route (straight lines between controls), assuming we would walk up to 50% more, i.e. around 30km, which would be OK for 8 hours.
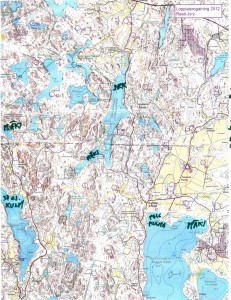
This event had a 1:25000 map which was much easier to read compared to the 1:40000 one last fall. No problems in the beginning, we fould 23 -> 21 -> 31 -> 41 quite easily. The first digit of the control-numnber indicates how many points you get for the control. The next control 51 was worth five points, and they are usually harder to find. Not this time, since it was at the very top of a hill, and people before us had already left tracks in the snow.
Then comes the big mistake of the day. We follow another faster group west down the hill from 51 towards 32. For some inexplicable reason we then completely mis-place ourselves on the map and although we are practically within reach of 32 we make a slow detour south before we realize where we are. Update: I have since learned that our confusion most probably was caused by a brand new road in this area, which was not marked on the map!
Probably annoyed by the first mistake, the second mistake of the day comes on the very next control: between 32 and 37 we take the wrong path north-east and decide to head back when we realize that.
So far we had stuck to the plan, but looking at the watch at 37 we decided to cut 39 from the route. Walk north along the road to 26, and then more walking along a big and then a small road to 57. At 57 we had some discussion about whether to walk back along the road, or try to find the electric lines north of 57 and let them guide us to the road. We had used 4 hours, or half of the total time here. We chose the latter route, and a straight northward pointing bit of our path after 57 indicates where we walked under the electric lines. Close to 53 the plan was to follow a path to the right of the hill and then the ditch to the control. Things didn't go to plan and we ended up to the left of the hill, but found the control with the help of tracks in the snow and voices/lights of others. A walk along the lake-shore to 55. And further north to a road.
So far we had roughly followed the plan. But now we had less than 3 hours left, and it was already dark making orienteering in the woods without clear paths or roads much harder. We decided to forget the plan and walk mostly along roads towards the finish, taking controls close to roads/paths along the way. A long bit of walking first south and then northeast to 49. Another long bit of walking all the way to 24. Here the image shows double GPS-paths because I switched from the 405cx watch to the Edge800 I use on the bike. We still had 45-50 minutes left at 24, so with a close eye on the clock we find 33 quite easily and 22 with a little more effort. We finished with about 12 minutes to spare.
About 90 teams (either solo, or in teams of 2-4 persons) took part.
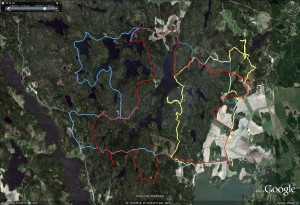
Update, here's our route again (in red), compared to another slightly faster team's route in blue: