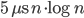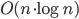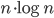Tag: benchmark

y-cruncher

I ran y-cruncher on a number of machines. Note the logarithmic y-axis. Lower is faster.

y-cruncher_results

  • i7-3537U, 2.5 years old Lenovo yoga laptop. Runs hot. Time to upgrade?
  • i5-4300U, ~1 year old work laptop, HP ultrabook. Runs much cooler.
  • i7-2600K, 3+ years old home desktop
  • i7-3770, 2.5 years old work desktop
  • Opteron 4334, Del R515 server, 1? year old.
  • i7-3930K, computing machine at work, 3+ years old
  • i7-5820K and i7-4770K newest lab computers, both 1 year old.

Random points VD benchmark

Here's some benchmark data for constructing the Voronoi diagram (or its dual, the Delaunay triangulation) for random point sites. Code for this benchmark is over here: https://github.com/aewallin/voronoi-benchmark

OpenVoronoi is my own effort using the incremental topology-oriented algorithm of Sugihara&Iri and Held. Floating-point coordinates with all sites falling within the unit-circle are used. Fast double-precision arithmetic is used for geometric predicates (e.g. "in-circle") during the incremental construction of the diagram, since the topology-oriented approach ensures that the algorithm finishes and produces an output graph regardless of errors in the geometric predicates. Quad-precision arithmetic is used for positioning vd-vertices. This benchmark runs in ca 7us*N*log2(N) time.

Boost.Polygon uses Fortune's sweepline algorithm. Only integer input coordinates are allowed, which ensures that geometric predicates can be computed exactly. Lazy arithmetic, where a high-precision slower number-type is used only when required, is used. This benchmark runs in ca 0.2us*N*log2(N) time.

CGAL uses exact geometric computation, which is slow but supposedly robust. The run-time gets worse with increasing problem-size and doesn't seem to fall on an O(N*log(N)) line.

Some thoughts:

  • OpenVoronoi is obviously too slow! Lazy arithmetic or other methods are required so that most vd-vertices can be positioned with fast double-precision code, and the quad-precision methods need to be called only rarely. OpenVoronoi uses a BGL adjacency_list to store the graph - this may also be too slow compared to a C-style "raw" data structure.
  • Other libraries which might be added to the benchmark: Triangle and QHull.
  • Held has, IIRC, reported around 0.5us*N*log2(N) for his closed-source VRONI algorithm. From the interwebs we also find this quote: "If your use is commercial, VRONI's license is a few thousand dollars."
  • It's easy to measure run-time, but how do we measure the correctness of the output that these algorithms produce? A first simple approach is write the output to a PNG or SVG file and visually inspect it, but something more precise and automated would be nice.
  • Neither Boost.Polygon nor OpenVoronoi support circular arc sites yet. Both can in principle be extended to do so.
  • Are we comparing apples to oranges? Is the output of these algorithms the same? OpenVoronoi produces a half-edge data structure of the diagram with edge-parametrizations (lines, parabolas) that allow computing a point on an edge at a given offset-distance from an adjacent site. The data structure allows for iterating through the edges, vertices, and faces of the graph.

 

Random line-segment voronoi diagram

Update3: version 11.10-148 now goes to 16k line-sites without errors or warnings:

Update2: This diagram with 8k vertices clearly has errors:

Update: Version 11.10-141 now copes with 4k random segments. But I don't know of any smart way to check the diagram for correctness..

Constructing the vd for random (non-crossing) line-segments is a reasonable stress-test for my vd-algorithm. When you've fixed one bug, just increase the number of line-segments by a factor of two and you will most likely uncover another! It now runs OK up to 2048 line-segments (yes, that does imply I get a segfault at 4096!).

There's some slowdown from 5us*n*log(n) in september 2011 (for just point-sites), to this code which runs in about 15 to 20us*n*log(n) when inserting the point-sites. Line-sites take longer, about 200us*m*log(m) for m line-sites.

vd benchmark

Tuesday update: A few optimizations has shaved about half off the constant, to 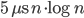. This was mainly (a) choosing boost::vecS as the out-edge container for the BGL-graph, and (b) choosing std::vector instead of std::set for a temporary variable in the grid-search for the closest facet. I suspect the runtime is dominated by that grid-search. Profiling would tell.

I did some benchmarking of my vd-code. It is supposed to run in 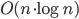time. Benchmarking turns out to be not so simple. I normally compile without any optimizations, and with a lot of sanity-checks and assert():s all over the code. These checks have worse time-complexity and result in long runtimes with big inputs. Then there are compiler optimization flags like -O or -O3.

I was first running the algorithm by inserting each point from python-code:

    t_before = time.time()
    for p in plist:
        vd.addVertexSite( p )
    t_after = time.time()
    return (t_after - t_before)

which I thought could add some overhead. I also made a version ("batch mode") where we first push all points to c++, and then call a run() method:

    for p in plist:
        vd.pushVertexSite( p )
    t_before = time.time()
    vd.run()
    t_after = time.time()
    return (t_after - t_before)

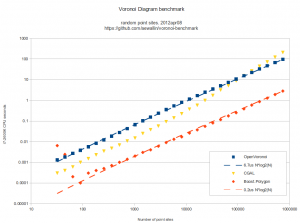
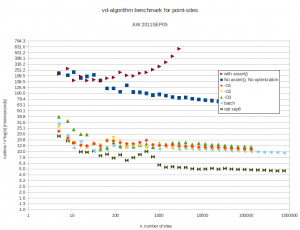
but this seems to improve runtime only marginally. Here are the results. Runtimes are divided by 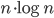, so ideally all points should fall on a horizontal line. At best the code now runs in about 10-16 microseconds times .

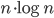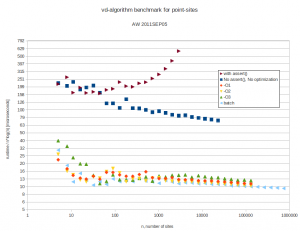
With 4096 input points the runtime improves from 12s down to 1.3s by turning off sanity-checks and assert():s. It further improves to 0.18s with -O3 and to 0.165s in batch-mode.

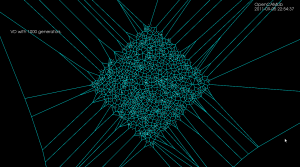
As an example, the voronoi diagram for 1000 random points looks like this: