How accurately can you in principle measure temperature with an RTD or thermistor?
If we push a current  through the resistor we'll get a voltage of
through the resistor we'll get a voltage of 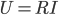 across it. Now as the temperature changes the resistance will change by
across it. Now as the temperature changes the resistance will change by 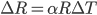 where
where  is the temperature coefficient of the sensor. This will give us a signal
is the temperature coefficient of the sensor. This will give us a signal
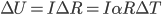
On the other hand the Johnson noise across the resistor will be
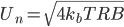 where B is the bandwidth, and we get a signal-to-noise ratio of
where B is the bandwidth, and we get a signal-to-noise ratio of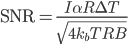
The noise-quivalent-temperature (NET) can be defined as
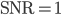 or
or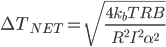
Here we can identify
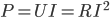 as the power dissipated in the resistor and simplify to
as the power dissipated in the resistor and simplify to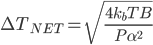
Here's a table with some common values for pt100 and 10k NTC thermistors. The sensitivity  is determined by the sensor type. What limits
is determined by the sensor type. What limits 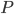 is self-heating of the sensor which probably should be kept to a few milli-Kelvins in most precision applications. Thermistors with their higher sensitivity are an obvious choice for high-resolution applications, but the lower
is self-heating of the sensor which probably should be kept to a few milli-Kelvins in most precision applications. Thermistors with their higher sensitivity are an obvious choice for high-resolution applications, but the lower  of a pt100 sensor can be compensated with a larger
of a pt100 sensor can be compensated with a larger 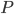 since most pt100 sensors are physically larger and thus have lower self-heating. pt100 sensors require 4-wire sensing, slightly more complex than a 2-wire measurement which is OK for a thermistor.
since most pt100 sensors are physically larger and thus have lower self-heating. pt100 sensors require 4-wire sensing, slightly more complex than a 2-wire measurement which is OK for a thermistor.
| Sensor | Resistance | Sensitivity (divide by R to get alpha!) | Dissipated Power P | Noise-Equivalent-Temperature (1Hz bandwidth) |
| pt100 | 100 Ohms | 0.391 Ohms/C | 100 uW (I=1mA) | 3 uK |
| NTC Thermistor | 10 kOhms | -500 Ohms/C | 9 uW (I=30uA) | 0.9 uK |
I conclude that it is not entirely obvious how to choose between a pt100 and a 10k thermistor. The thermistor is intrinsically more sensitive, but with good thermal contact to its surroundings self-heating in a pt100 sensor can be minimized and the same noise-requivalent-temperature achieved. In any case it looks like Johnson noise limits resolution to 1 uK or so in a 1 Hz bandwidth. If we AD-convert the voltage at 24-bit resolution (16M states) we can get a reasonable measurement range of ~32 K by matching 1 LSB = 2 uK.
Does anyone know of similar back-of-the-envelope calculations for other sensors (Thermocouples, AD590)?
I think that the shot noise of the polarizing current Ipol (current noise) 2*Q*Ipol should be also mentioned. This current noise is larger than the Johnson-Nyquist noise (voltage noise) since R*Ipol = 100mV (52mV rule) However, if the polarization current Ipol is provided through the amplifier, it can be decorrelated (see bolometers set-ups)
In practicle, the voltage noise of the amplifier will be dominant. This voltage noise has a certain1/f component. In one word, it seems difficult to have a noise less than 10µ°K/Root(Hz)
In addition NTC thermistors are typically fabricated from metal oxides which have their own set of noise characteristics. Lastly, even if there is no metal oxide material noise if there is thermal noise in the system then that will be exhibited as voltage noise as transduced by the sensor itself.