Recursion and 'divide-and-conquer' must be two of the greatest ideas ever in computer science.
Threw together some code in python today for building an octree, given a function isInside() which the tree-builder evaluates to see if a node is inside or outside of the object. Nodes completely outside the interesting volume(here a sphere, for simplicity) are rendered grey. Nodes completely inside the object are coloured, green for low tree-depth, and red for high. Where the algorithm can't decide if the node is inside or outside we subdivide (until we reach a decision, or the maximum tree depth).
In the end our sphere-approximation looks something like this:

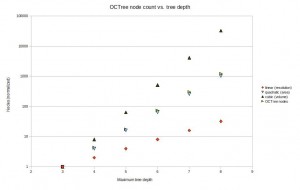
These tests were done with a maximum tree depth of 6 or 7. If we imagine we want a 100 mm long part represented with 0.01 mm precision we will need about depth 14, or a subdivision into 16384 parts. That's impractical to render right now, but seems doable. In terms of memory-use, the octree is much better than a voxel-representation where space is uniformly subdivided into tiny voxels. The graph below shows how the number of nodes grows with tree-depth in the actual octree, versus a voxel-model (i.e. a complete octree). For large tree-depths there are orders-of-magnitude differences, and the octree only uses a number of nodes roughly proportional to the surface area of the part.
Now, the next trick is to implement union (addition) and difference (subtraction) operations for octrees. Then you represent your stock material with one octree, and the tool-swept-volume of your machining operation with another octree -> lo and behold we have a cutting-simulator!
Back in the day when I was writing "simple" programs to solve similar things, we used, besides backtracking and divide and conquer, another approach called "dynamic programming" (loosely translated).
For example finding a way through a maze:
The idea is that you have the current state (a list of locations), and you make a list with all possible locations you can reach from the current locations. After excluding the ones you already visited, you append it to current location (and remove the ones already done). This way you can blaze through really large data types (e.g. a maze of 100x100 - that would take a lot using recursion and backtracking, takes a infinite shorter time using PD).
Maybe it's something to consider in this case too.