I need this seldom enough to forget how it's done - but then it's annoying to have to think/google for the solution again when I do need it... So I'll document here.
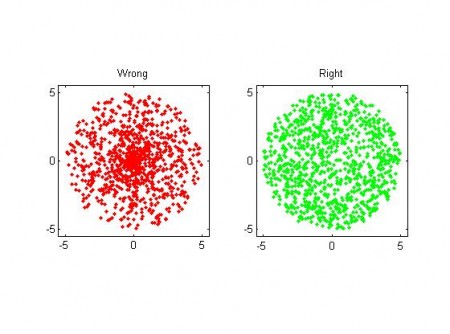
The task is to generate uniformly distributed numbers within a circle of radius R in the (x,y) plane. At first polar coordinates seems like a great idea, and the naive solution is to pick a radius r uniformly distributed in [0, R], and then an angle theta uniformly distributed in [0, 2pi]. BUT, you end up with an exess of points near the origin (0, 0)! This is wrong because if we look at a certain angle interval, say [theta, theta+dtheta], there needs to be more points generated further out (at large r), than close to zero. The radius must not be picked from a uniform distribution, but one that goes as
pdf_r = (2/R^2)*r
That's easy enough to do by calculating the inverse of the cumulative distribution, and we get for r:
r = R*sqrt( rand() )
where rand() is a uniform random number in [0, 1]. Here is a picture:
some matlab code here.
The thinking for generating random points on the surface of a sphere in 3D is very similar. If I get inspired I will do a post on that later, meanwhile you can go read these lecture notes.
Why is pdf_r= (2/R^2)*r ?
In polar coordinates an infinitesimal area-element is: dr * r * dtheta
if we want points uniformly distributed in this area the pdf for r should "clearly" be proportional to r.
we also want the pdf to be normalized so that the integral from 0 to R of the pdf is 1. That leads to the pre-factor (2/R^2)
Thanks. I too made the mistake but realized later that it would be more concentrated closer to the origin.
Your code could be a lot more efficient by vectorizing instead of looping:
% prepare
Nmax = 1e3;
R = 5;
% Wrong
r1 = R*rand(Nmax,1);
theta1 = 2*pi*rand(Nmax,1);
x1 = r1.*cos(theta1);
y1 = r1.*sin(theta1);
% Right
r2 = R*sqrt(rand(Nmax,1));
theta2 = 2*pi*rand(Nmax,1);
x2 = r2.*cos(theta2);
y2 = r2.*sin(theta2);
% plot it
subplot(1,2,1);
plot(x1, y1, 'r.');
axis square
title('Left')
subplot(1,2,2);
plot(x2, y2, 'g.');
axis square
title('Right')
Why not just pick a random x between 0 and R and then a random Y between 0 and sqrt(R^2 - x^2)
I think that creates an excess of points at higher x-values, for the same reason as simple polar coordinates don't work - i.e. the probability per unit area isn't constant if you pick x=rand(0,1) and y=rand(0,sqrt(R*R-x*x))
try the python code below:
import matplotlib.pyplot as plt
import numpy
R=1.0
nmax=int(1e4)
x = numpy.random.rand(nmax,1)
ymax = numpy.sqrt(R*R-x*x)
y = ymax*numpy.random.rand(nmax,1)
print x
plt.figure()
plt.plot(x,y,'.')
plt.title('x=rand(0, 1), y = rand(0, sqrt(R*R-x*x))')
plt.show()
the vectoring instead of looping as shown by Evan is actually very effective to decrease the FLOPs of your code ...how ever i am getting the warning "Warning: Size vector should be a row vector with integer elements. "Warning: Size vector should be a row vector with integer elements. " for
r1 = R*rand(Nmax,1);
theta1 = 2*pi*rand(Nmax,1);
and
r2 = R*sqrt(rand(Nmax,1));
theta2 = 2*pi*rand(Nmax,1);
i know it can be ignored but its annoying me as to why am i getting it. any suggestions to overcome it?
Mariam: It's hard to say but my guess is you have something non-integer in the "Nmax" variable.
As the rest of you here sound to be either math professors/majors or at least much more mathmatically versed than myself can someone explain this in layman's terms and/or write a step by step guide as to where to put the radius, amount of points, etc an how to calculate it.
Thanks for the help! I had need of a uniform distribution inside an annulus (see the 'half-moon' classification in Neural Networks and Learning Machines by Haykin). Generalizing your result to the case of an annulus of inner radius A and outer radius B, I get
r = sqrt( rand() × (B^2 − A^2) + A^2 )
This page lists a few approaches to generating random points within a sphere:
https://math.stackexchange.com/questions/87230/picking-random-points-in-the-volume-of-sphere-with-uniform-probability
Hi,
I understand the PDF of r, but, based on it, how do you find that transformation from rand() ? Can you explain that more in details ?
thanks