I need this seldom enough to forget how it's done - but then it's annoying to have to think/google for the solution again when I do need it... So I'll document here.
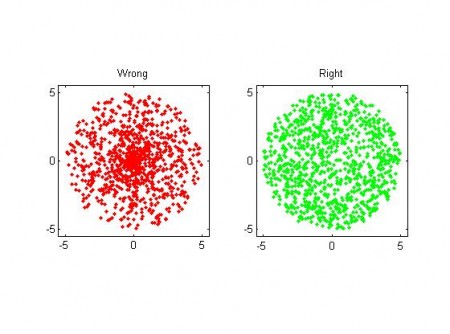
The task is to generate uniformly distributed numbers within a circle of radius R in the (x,y) plane. At first polar coordinates seems like a great idea, and the naive solution is to pick a radius r uniformly distributed in [0, R], and then an angle theta uniformly distributed in [0, 2pi]. BUT, you end up with an exess of points near the origin (0, 0)! This is wrong because if we look at a certain angle interval, say [theta, theta+dtheta], there needs to be more points generated further out (at large r), than close to zero. The radius must not be picked from a uniform distribution, but one that goes as
pdf_r = (2/R^2)*r
That's easy enough to do by calculating the inverse of the cumulative distribution, and we get for r:
r = R*sqrt( rand() )
where rand() is a uniform random number in [0, 1]. Here is a picture:
some matlab code here.
The thinking for generating random points on the surface of a sphere in 3D is very similar. If I get inspired I will do a post on that later, meanwhile you can go read these lecture notes.