Drop Cutter part 1/3: Cutter vs. Vertex

Based on a 2002 paper by Chuang et al., I'm trying to understand the math for calculating 'drop-cutter' toolpaths (Julian Todd also has a lot to say about the drop-cutter approach). The basic idea is that the x,y position of the cutter is known, and it is dropped down along the z-axis until it touches a triangulated surface. A complex surface is built up of many many small triangles, but the algorithm stays the same.

For each triangle there are seven items the cutter might be touching: three vertices, three edges, and one facet (the triangle surface). It looks like a contact point with a vertex is the easiest to calculate, so I'm starting with that. I'm hoping to post part 2/3 and 3/3 of this post soon. They will deal with the facet and the edges.

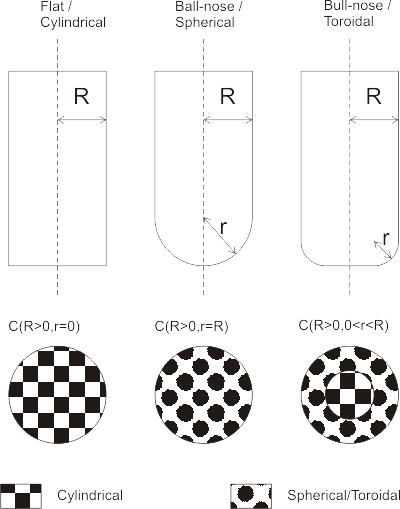
I'm using this fairly simple cutter definition C(R,r) where R denotes the shaft diameter and r the corner radius. The three basic shapes that can be defined this way are shown in the picture. A more elaborate model would include tapered cutters, but I think I won't bother with that now... A cutter thus consists of a cylindrical part or a toroidal part, or both. That means I need six different functions in total for this algorithm:

1. Cylinder against vertex
2. Toroid against vertex
3. Cylinder against facet
4. Toroid against facet
5. Cylinder against edge
6. Toroid against edge

Here's how I think no 1 and 2 work.

Assume the vertex we are testing against is at (x, y, z) and say the cutter is at location xe,ye. We are looking for the cutter z-coordinate ze so at the end when the cutter is in contact with the vertex it will be located at (xe, ye, ze) .

Calculate the distance in the xy-plane from (xe, ye) to (x, y):
q = sqrt( (xe-x)^2 + (ye-y)^2)

Now if q > R the vertex lies outside the cutter and we should report an error or just skip to the next triangle/vertex.

If q <= R-r the vertex lies under the cylindrical part of the cutter and we set ze = z

If (R-r) < q <= R the vertex lies under the spherical/toroidal part of the cutter. This picture should explain the geometry:

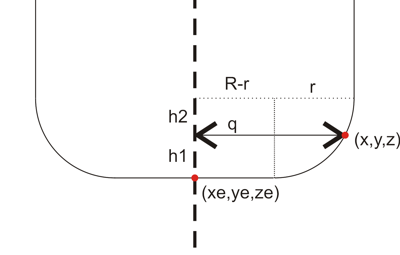
The cutter can be positioned a distance z1 lower than z. To calculate z1 we need z2. It can be found by noting that (x ,y, z) should lie on the toroidal surface:
(q-(R-r))^2 + h2^2 = r^2
or h2 = sqrt( r^2 - (q-(R-r))^2 )
so now h1=r-h2 and we found ze = z-h1

A quick test in matlab seems to confirm that this works:

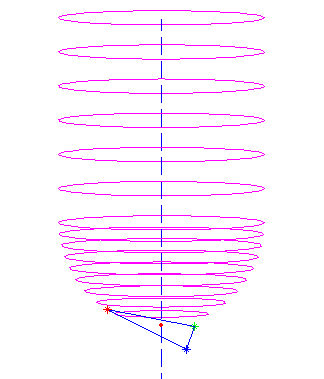
here a ball-nose cutter is dropped down along the dashed line into contact with all three vertices (red, blue, and green stars), and finally it's positioned at the highest ze found (red dot).

Well, that was easy. Now onto the facet and edge tests!