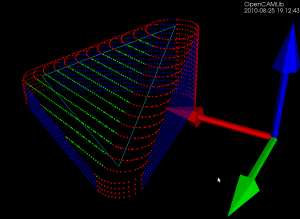
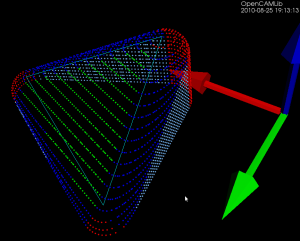
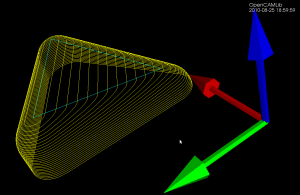
The basic operation when producing waterline-paths is to push the cutter along either the X or Y axis (red and green arrows) into contact with a triangle (cyan lines). That's done through three different functions, one each for the vertices, facet, and edges of the triangle. The vertex test (results shown as red dots) and the facet test (green dots) are straightforward to implement. The edge-test (blue dots) is more involved. The above figure is for a CylCutter where the edge-test is implemented through the vertex-test (thus red dots along the edges), but this figure for a BallCutter shows the colors better:
Blue dots show edge-contacts with the spherical part of the cutter, light-blue dots show edge-contacts with the cylindrical shaft of the cutter.
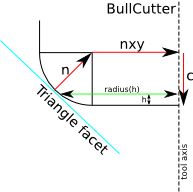
The vertex test requires only a radius(h) function that returns the radius of the cutter at height h. The facet test needs three parameters (n, nxy, c) for each cutter, which define where the cutter should be located relative to a point which lies on the facet. From the CC-point on the facet we go a distance n along the 3D unit-normal, then a distance nxy along a unit-normal in the XY-plane to find the cutter center. From the cutter center we go down along the z-axis by a distance c to find the CL-point.
Figuring out the (n,nxy,c) parameters for CylCutter and BallCutter is left as an exercise for the reader.
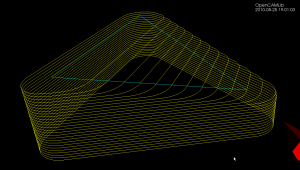
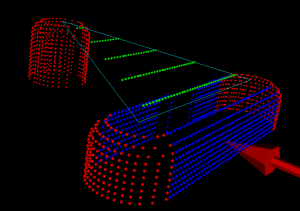
These points are then hooked up in the correct order to produce waterlines like this (CylCutter on the left, BallCutter on the right).
The edge-test for CylCutter reduces to a 2D problem of line-line intersections, while the edge-test for BallCutter can be done by intersecting a cylinder/tube around the edge with a line. The filleted/toroidal/BullCutter edge-test is much harder. Here I've just implemented the special case where the edge is horizontal and the solution is easy to find analytically. The general case where the edge slopes up or down requires an iterative solution to either a quartic or the offset-ellipse problem.