If you have lots and lots of holes to drill on your cnc-machine you might want a TSP solver to optimize the order of the holes so as to minimize rapid movements between holes. I've written a small wrapper around metric_tsp_approx from the boost graph library and included it in opencamlib as a new class TSPSolver. Here's an example on problem "u2152" from TSPLIB95.
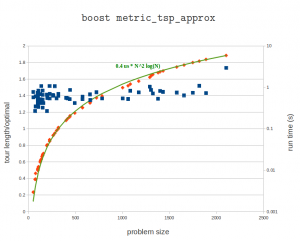
Here's a plot of the tour length compared to the known optimal tour length, as well as the run-time on my laptop (P9400 CPU). These problems range in size from 51 points to 2103 points. I might run the bigger problems on the desktop machine later. The algorithm guarantees a tour which is at worst twice the length of the optimal tour. In practice the solutions seem to scatter around 1.4 or 1.5 times the length of the optimal tour. The run times fall neatly on the predicted O(N²*log(N) curve.
A simple greedy heuristic (with better run-time?) which always selects the closest unvisited point also guarantees a tour at most twice the length of the optimal tour.
There's also a better heuristic, the Christofides algorithm, which guarantees a tour length at most 1.5 times the optimal tour length. In addition to the minimum-spanning-tree algorithm it requires a minimum cost perfect matching algorithm. I'm not sure if there is open-source code for this somewhere.
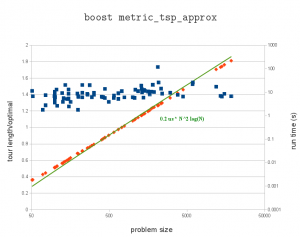
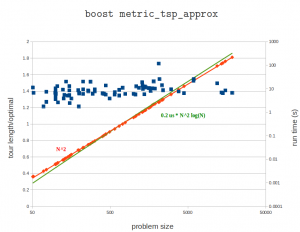
Update: here's a run on an i7-2600K cpu. The pre-factor is now halved to about 0.2 microseconds. The largest problem has 18512 cities and takes over three minutes (217 seconds) to solve.
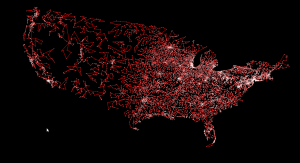
Here's 'usa13509' from TSPLIB. Cities with population at least 500 in the continental US. Presumably from 1995 or so.
Scaling (?)