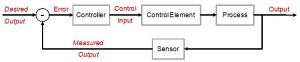
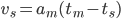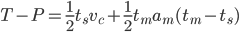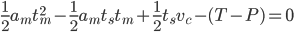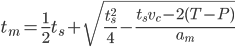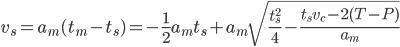Tag: trajectory

Simple Trajectory Generation

image4_w

The world is full of PID-loops, thermostats, and PLLs. These are all feedback loops where we control a certain output variable through an input variable, with a more or less known physical process (sometimes called "plant") between input and output. The input or "set-point" is the desired output where we'd like the feedback system to keep our output variable.

Let's say we want to change the set-point. Now what's a reasonable way to do that? If our controller can act infinitely fast we could just jump to the new set-point and hope for the best. In real life the controller, plant, and feedback sensor all have limited bandwidth, and it's unreasonable to ask any feedback system to respond to a sudden change in set-point. We need a Trajectory - a smooth (more or less) time-series of set-point values that will take us from the current set-point to the new desired value.

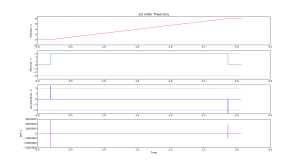
Here are two simple trajectory planners. The first is called 1st order continuous, since the plot of position is continuous. But note that the velocity plot has sudden jumps, and the acceleration & jerk plots have sharp spikes. In a feedback system where acceleration or jerk corresponds to a physical variable with finite bandwidth this will not work well.

1st_order_trajectory

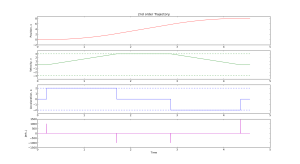
We get a smoother trajectory if we also limit the maximum allowable acceleration. This is a 2nd order trajectory since both position and velocity are continuous. The acceleration still has jumps, and the jerk plot shows (smaller) spikes as before.

2nd_order_trajectory

Here is the python code that generates these plots:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196

# AW 2014-03-17
# GPLv2+ license
 
import math
import matplotlib.pyplot as plt
import numpy
 
# first order trajectory. bounded velocity.
class Trajectory1:
	def __init__(self, ts = 1.0, vmax = 1.2345):
		self.ts = ts		# sampling time
		self.vmax = vmax	# max velocity
		self.x = float(0)	# position
		self.target = 0
		self.v = 0 			# velocity
		self.t = 0			# time
		self.v_suggest = 0
 
	def setTarget(self, T):
		self.target = T
 
	def setX(self, x):
		self.x = x
 
	def run(self):
		self.t = self.t + self.ts	# advance time
		sig = numpy.sign( self.target - self.x ) # direction of move
		if sig > 0:
			if self.x + self.ts*self.vmax > self.target:
				# done with move
				self.x = self.target
				self.v = 0
				return False
			else:
				# move with max speed towards target
				self.v = self.vmax
				self.x = self.x + self.ts*self.v
				return True
		else:
			# negative direction move
			if self.x - self.ts*self.vmax < self.target:
				# done with move
				self.x = self.target
				self.v = 0
				return False
			else:
				# move with max speed towards target
				self.v = -self.vmax
				self.x = self.x + self.ts*self.v
				return True
 
	def zeropad(self):
		self.t = self.t + self.ts
 
	def prnt(self):
		print "%.3f\t%.3f\t%.3f\t%.3f" % (self.t, self.x, self.v )
 
	def __str__(self):
		return "1st order Trajectory."
 
# second order trajectory. bounded velocity and acceleration.
class Trajectory2:
	def __init__(self, ts = 1.0, vmax = 1.2345 ,amax = 3.4566):
		self.ts = ts
		self.vmax = vmax
		self.amax = amax
		self.x = float(0)
		self.target = 0
		self.v = 0 
		self.a = 0
		self.t = 0
		self.vn = 0 # next velocity
 
	def setTarget(self, T):
		self.target = T
 
	def setX(self, x):
		self.x = x
 
	def run(self):
		self.t = self.t + self.ts
		sig = numpy.sign( self.target - self.x ) # direction of move
 
		tm = 0.5*self.ts + math.sqrt( pow(self.ts,2)/4 - (self.ts*sig*self.v-2*sig*(self.target-self.x)) / self.amax )
		if tm >= self.ts:
			self.vn = sig*self.amax*(tm - self.ts)
			# constrain velocity
			if abs(self.vn) > self.vmax:
				self.vn = sig*self.vmax
		else:
			# done (almost!) with move
			self.a = float(0.0-sig*self.v)/float(self.ts)
			if not (abs(self.a) <= self.amax):
				# cannot decelerate directly to zero. this branch required due to rounding-error (?)
				self.a = numpy.sign(self.a)*self.amax
				self.vn = self.v + self.a*self.ts
				self.x = self.x + (self.vn+self.v)*0.5*self.ts
				self.v = self.vn
				assert( abs(self.a) <= self.amax )
				assert( abs(self.v) <= self.vmax )
				return True
			else:
				# end of move
				assert( abs(self.a) <= self.amax )
				self.v = self.vn
				self.x = self.target
				return False
 
		# constrain acceleration
		self.a = (self.vn-self.v)/self.ts
		if abs(self.a) > self.amax:
			self.a = numpy.sign(self.a)*self.amax
			self.vn = self.v + self.a*self.ts
 
		# update position
		#if sig > 0:
		self.x = self.x + (self.vn+self.v)*0.5*self.ts
		self.v = self.vn
		assert( abs(self.v) <= self.vmax )
		#else:
		#	self.x = self.x + (-vn+self.v)*0.5*self.ts
		#	self.v = -vn
		return True
 
	def zeropad(self):
		self.t = self.t + self.ts
 
	def prnt(self):
		print "%.3f\t%.3f\t%.3f\t%.3f" % (self.t, self.x, self.v, self.a )
 
	def __str__(self):
		return "2nd order Trajectory."
 
vmax = 3 # max velocity
amax = 2 # max acceleration
ts = 0.001 # sampling time
 
# uncomment one of these:
#traj = Trajectory1( ts, vmax )
traj = Trajectory2( ts, vmax, amax )
 
traj.setX(0) # current position
traj.setTarget(8) # target position
 
# resulting (time, position) trajectory stored here:
t=[]
x=[]
 
# add zero motion at start and end, just for nicer plots
Nzeropad = 200
for n in range(Nzeropad):
	traj.zeropad()
	t.append( traj.t )
	x.append( traj.x ) 
 
# generate the trajectory
while traj.run():
	t.append( traj.t )
	x.append( traj.x ) 
t.append( traj.t )
x.append( traj.x )
 
for n in range(Nzeropad):
	traj.zeropad()
	t.append( traj.t )
	x.append( traj.x ) 
 
 
# plot position, velocity, acceleration, jerk
plt.figure()
plt.subplot(4,1,1)
plt.title( traj )
plt.plot( t , x , 'r')
plt.ylabel('Position, x')
plt.ylim((-2,1.1*traj.target))
 
plt.subplot(4,1,2)
plt.plot( t[:-1] , [d/ts for d in numpy.diff(x)] , 'g')
plt.plot( t , len(t)*[vmax] , 'g--')
plt.plot( t , len(t)*[-vmax] , 'g--')
plt.ylabel('Velocity, v')
plt.ylim((-1.3*vmax,1.3*vmax))
 
plt.subplot(4,1,3)
plt.plot( t[:-2] , [d/pow(ts,2) for d in numpy.diff( numpy.diff(x) ) ] , 'b')
plt.plot( t , len(t)*[amax] , 'b--')
plt.plot( t , len(t)*[-amax] , 'b--')
plt.ylabel('Acceleration, a')
plt.ylim((-1.3*amax,1.3*amax))
 
plt.subplot(4,1,4)
plt.plot( t[:-3] , [d/pow(ts,3) for d in numpy.diff( numpy.diff( numpy.diff(x) )) ] , 'm')
plt.ylabel('Jerk, j')
plt.xlabel('Time')
 
plt.show()

See also:

I'd like to extend this example, so if anyone has simple math+code for a third-order or fourth-order trajectory planner available, please publish it and comment below!

EMC2 tpRunCycle revisited

I started this EMC2 wiki page in 2006 when trying to understand how trajectory control is done in EMC2. Improving the trajectory controller is a topic that comes up on the EMC2 discussion list every now and then. The problem is just that almost nobody actually takes the time and effort to understand how the trajectory planner works and documents it...

A recent post on the dev-list has asked why the math I wrote down in 2006 isn't what's in the code, so here we go:

I will use the same shorthand symbols as used on the wiki page. We are at coordinate P ("progress") we want to get to T ("target") we are currently travelling at vc ("current velocity"), the next velocity suggestion we want to calculate is vs ("suggested velocity), maximum allowed acceleration is am ("max accel") and the move takes tm ("move time") to complete. The cycle-time is ts ("sampling time"). The new addition compared to my 2006 notes is that now the current velocity vc as well as the cycle time ts is taken into account.

As before, the area under the velocity curve is the distance we will travel, and that needs to be equal to the distance we have left, i.e. (T-P). (now trying new latex-plugin for math:) (EQ1)

Note how the first term is the area of the red triangle and the second therm is the area of the green triangle. Now we want to calculate a new suggested velocity vs so that using the maximum deceleration our move will come to a halt at time tm, so(EQ2):


Inserting this into the first equation gives (EQ3):


this leads to a quadratic eqation in tm (EQ4):


with the solution (we obviously want the plus sign)(EQ5)


which we can insert back into EQ2 to get (EQ6) (this is the new suggested max velocity. we obviously apply the accel and velocity clamps to this as noted before)


It is left as an (easy) exercise for the reader to show that this is equivalent to the code below (note how those silly programmers save memory by first using the variable discr for a distance with units of length and then on the next line using it for something else which has units of time squared):

discr = 0.5 * tc-&gt;cycle_time * tc-&gt;currentvel - (tc-&gt;target - tc-&gt;progress);
discr = 0.25 * pmSq(tc-&gt;cycle_time) - 2.0 / tc-&gt;maxaccel * discr;
newvel = maxnewvel = -0.5 * tc-&gt;maxaccel * tc-&gt;cycle_time +tc-&gt;maxaccel * pmSqrt(discr);

over and out.