Tag: time and frequency

CONT vs RCON mode on the 53230A frequency counter

This is a follow-up to my earlier notes on the 53230A noise floor.

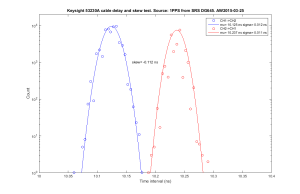
Naively I did the initial frequency-counting tests using READ?, which is wrong both because it produces data with dead-time and because the consensus for what is meant by Allan deviation assumes pi-counting.

Driven by marketing, no doubt, the 53230A employs internal averaging (something akin to lambda-counting) both with the simple READ? command and the continuous CONT mode mentioned in the manual. Amazingly you have to use the undocumented RCON mode to get pi-counting which will produce correct Allan deviations.

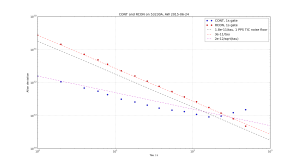
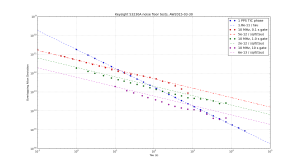
Here is a plot. The opportunity for making errors (with pi- vs. lamda-counting, and gap-free data) is less in time-interval mode, and I have indicated the 12 ps RMS noise floor (1.8e-11/tau in terms of Allan deviation) with a black dashed line. In RCON mode the noise floor has the same 1/tau dependence and I get about 3e-11/tau. If however you simply use the built-in settings of the counter with READ? or CONT you get a noise floor of about 2e-12/sqrt(tau) due to the internal averaging going on behind the scenes.

RCON_vs_CONT

For a paper that explains pi- and lambda-counting see Dawkins2007 (fulltext PDF on ReaserchGate). Enrico Rubiola also has notes on counters.

Datafiles and script for ADEV and figure: 2015-06-18_rcon_cont.zip

Keysight 53230A noise floor test

We got a new 53230A counter to the lab, so I decided to run some basic tests on it.

I collected time interval data using a 1-PPS source (H-maser through a SRS DG645), and wired this with a T-connector from CH1 to CH2 with a ~1 m (10 ns delay) cable. This should show the noise floor for time interval measurements as well as CH1/CH2 timing skew when measured the other way around (i.e. from CH2 to CH1). The 10 MHz external reference (at the back) was connected to a H-maser.

53230A_PPS_skew
The results show standard deviations of 12 ps (CH1->CH2) and 11 ps (CH2->CH1) respecively, with a channel skew of 112 ps. Compare to the single-shot spec of sqrt(2)*20 ps = 28 ps and Agilent/Keysight's marketing video on youtube.

I also collected 10 MHz frequency counter readings on CH1 (source: H-maser) with gate times of 0.1 s, 1.0 s, and 10.0 s. I collected the data with a simple program that just calls the "READ?" function repeatedly, which does result in some dead-time between measurements.

Here are the results in terms of Allan deviation. I used allantools.

Keysight_53230A_noise_floor

The time interval noise floor looks like white phase noise with an Allan deviation of 1.8e-11/tau. This is consistent with the 12 ps RMS value found above. It is left as an exercise for the reader to show that ADEV(1s) = sqrt(3)*RMS-time-interval-noise (correct??).

The frequency counting noise floor depends on the gate time, and I get 5e-12/sqrt(tau), 2e-12/sqrt(tau), and 6e-13/sqrt(tau) for gate times of 0.1 s, 1.0 s, and 10.0 s, respectively. This looks like white frequency noise. Enrico Rubiola has notes on frequency counters that may explain the numbers.