Here's an experiment I've done recently:
(Time-lapse of ca 18 hour experiment. Bottom left is a spectrum-analyzer view of the beat-note signal. Top left is a frequency counter reading of the beat-note. Bottom right is a screen showing the a camera-view of the output-beam from the resonator)
This is a measurement of the thermal expansion of a fancy optical resonator made from Corning "Ultra Low Expansion" (ULE) glass. This material has a specified thermal expansion of 0.03 ppm/K around room temperature. This thermal expansion is roughly 800-times smaller than Aluminium, around 400-times smaller than Steel, and 40-times better than Invar - a steel grade specifically designed for low thermal expansion.
Can we do even better? Yes! Because ULE glass has a coefficient of thermal expansion (CTE) that crosses zero. Below a certain temperature it shrinks when heated, and above the zero-crossing temperature it expands when heated (like most materials do). This kind of behavior sounds exotic, but is found is something as common as water! (water is heaviest at around 4 C). If we can use the ULE resonator at or very close to this magic zero-crossing temperature it will be very very insensitive to small temperature fluctuations.
So in the experiment I am changing the temperature of the ULE glass and looking for the temperature where the CTE crosses zero (let's call this temperature T_ZCTE). The effect is fairly small: if we are 1 degree C off from T_ZCTE we would expect the 300 mm long piece of ULE glass to be 200 pm (picometers) longer than at T_ZCTE. That's about the size of a single water-molecule, so this length change isn't exactly something you can go and measure with your digital calipers!
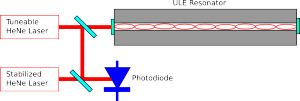
Here's how it's done (this drawing is simplified, but shows the essential parts of the experiment):
We take a tuneable HeNe laser and lock the frequency of the laser to the ULE-cavity. The optical cavity/resonator is formed between mirrors that are bonded to the ends of the piece of ULE glass. We can lock the laser to one of the modes of the cavity, corresponding to a situation where (twice) the length of the cavity is an integer number of wavelenghts. Now as we change the temperature of the ULE-glass the laser will stay locked, and as the glass shrinks/expands the wavelength (or frequency/color) of the laser will change slightly.
Directly measuring the frequency of laser light isn't possible. Instead we take second HeNe laser, which is stabilized to have a fixed frequency, and detect a beat-note between the stabilized laser and the tuneable laser. The beat-note will have a frequency corresponding to the (absolute value of the) difference in frequency between the two lasers. Now measuring a length-change corresponding to the size of a single water-molecule (200 pm) shouldn't be that hard anymore!
Let's say the stabilized laser has a wavelength of 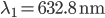 (red light). Its frequency will be
(red light). Its frequency will be 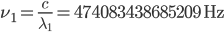 (that's around 474 THz). When the tuneable laser is locked to the cavity we force its wavelength to agree with
(that's around 474 THz). When the tuneable laser is locked to the cavity we force its wavelength to agree with 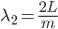 where
where  is an integer and
is an integer and  is the length of the cavity. I've drawn only a small number of wavelengths in the figure, but a realistic integer is
is the length of the cavity. I've drawn only a small number of wavelengths in the figure, but a realistic integer is  . We get
. We get 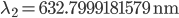 and
and 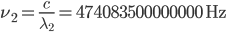 , very nearly but not quite the same wavelength/frequency as the stabilized laser. Now our photodiode which measures the beat-note will measure a frequency of
, very nearly but not quite the same wavelength/frequency as the stabilized laser. Now our photodiode which measures the beat-note will measure a frequency of 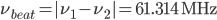 .
.
How does this change when the ULE glass expands by 200 pm? When we heat or cool the cavity by 1 degree C the length changes to 300 mm + 200 pm, and the wavelength of the tuneable laser will change to
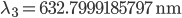 . Now our beat-note detector will show
. Now our beat-note detector will show 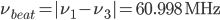 . That's a change in the beat-note of more than 300 kHz - easily measurable!
. That's a change in the beat-note of more than 300 kHz - easily measurable!
That's how you measure a length-change corresponding to the diameter of a water molecule!
Why do this? Some of the best ultra-stable lasers known are made by locking the laser to this kind of ULE-resonator. Narrow linewidth ultra-stable lasers are interesting for a host of atomic physics and other fundamental physics experiments.
See also: Janis Alnis playing with two ultra-stable lasers.
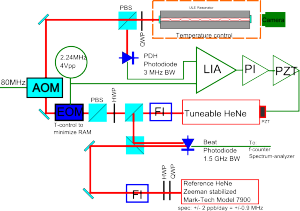
Update 2013 August: I made a drawing in inkscape of the experimental setup.
This figure shows most (if not all?) of the important components of this experiment. The AOM is not strictly required but I found it useful to shift the tuneable HeNe laser by +80 MHz to reach a TEM-00 mode of the ULE resonator. Not shown is a resonance-circuit (LC-tank) between the 2.24MHz sinewave-generator and the EOM. The EOM was temperature controlled by a TEC with an NTC thermistor giving temperature feedback.