Long time no blog..
Five days of skiing in Äksälomopolo, punctuated by two days of Norovirus 🙁
Great winter weather, possibly because of the early dates for Easter this year.
Äkäslompolo 2024
Crystek CVCO55 VCO
Cliff horizontal 4mm shrouded Banana connector
Amphenol vertical BNC connector
Bourns PTV09A-1 potentiometer footprint fix
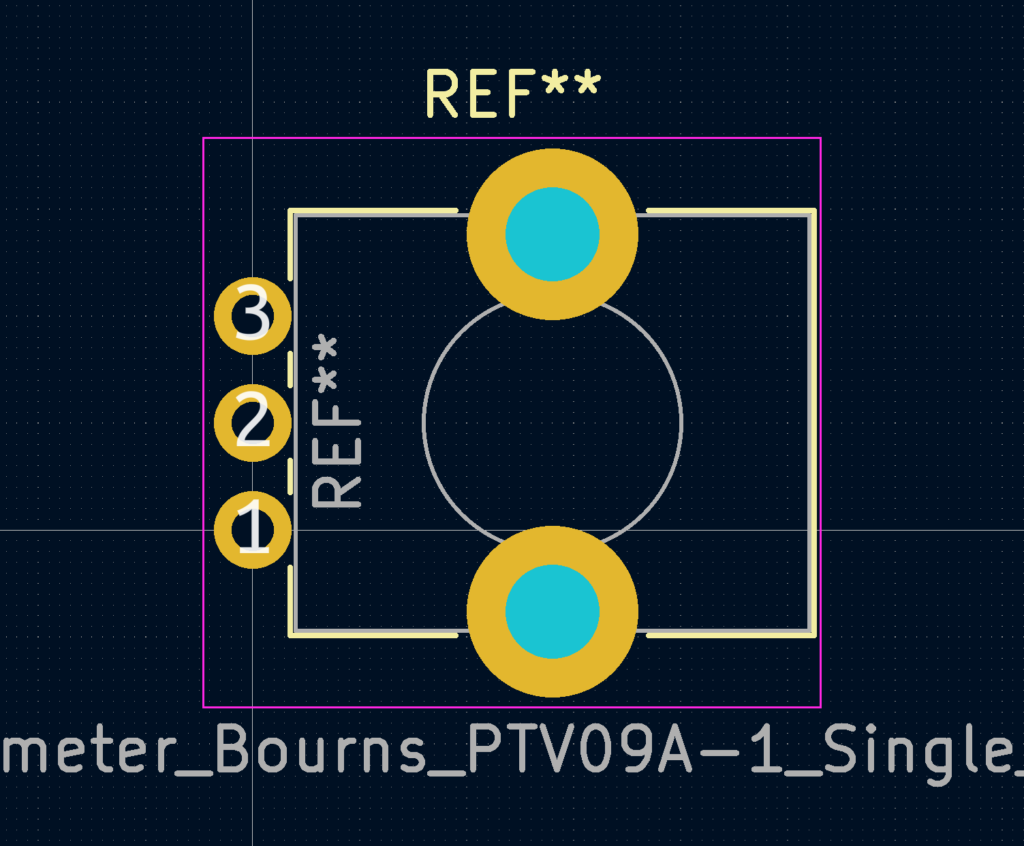
This footprint had too small mounting holes, and the potentiometer-shaft in the wrong place. https://gitlab.com/kicad/libraries/kicad-footprints/-/merge_requests/2991
ID.3 OTA update 2.3
First larger firmware update for the Voltswagen. For details see Battery Life or ID.Furkan or Schräg.
First part of update downloading 
First part installed 
Second part downloading 
Second part installed 
Done!
EVSE
ID Charger pro EVSE for the new Voltswagen.
Itärastit Landbo
Mistakes on #4 and #8 - slow terrain.
250MHz detector with Fermionics FD80FC photodiode
Here's anoter one-inch-photodetector with a Fermionics FD80FC photodiode and 5k1 transimpedance. Bandwidth around 250 MHz. Predicted dark noise and frequency response with TIASim. The Fermionics diode has a capacitance of only 0.4 pF (80 um diameter active area), giving slightly better bandwidth than a Thorlabs FGA01FC (2 pF capacitance, 120 um diameter active area).
Measured frequency response, compared to TIASim prediction
Iltarastit Solvalla
Sunshine and maybe +11..13C.