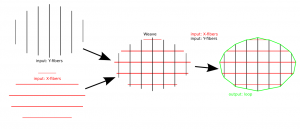
weave – anderswallin.net

Weave notes

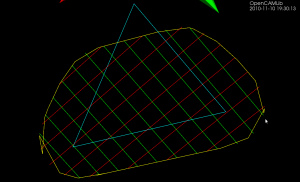
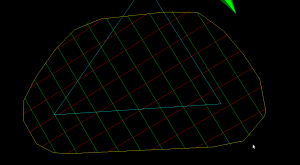
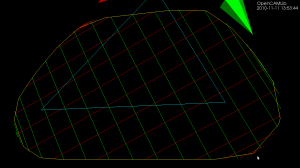
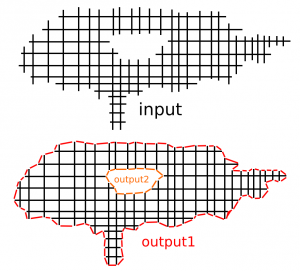
As noted before, the waterline operation consists of radial cutter projection ("push cutter") along fibers/dexels, followed by a weave/grid construction, and contouring to produce the final toolpath. Like so:

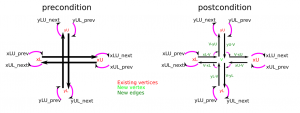
The new Weave2 class builds up a half-edge diagram in a smart way, maintaining "next" and "previous" pointers for each edge, so that the green toolpath loop can easily be found by traversing from one CL-point to the next simply following the "next" pointer:

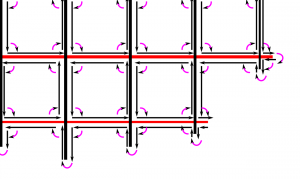
(The magenta arrows are "next" pointers which point from one edge to the next)

The main part of the algorithm looks at one X-fiber (from xL to xU) and one Y-fiber (from yL to yU) at a time and inserts a new internal vertex (v) into the diagram, while maintaining the existing "next" and "prev" pointers.

I didn't come up with any elegant object-oriented scheme that would do this nicely, so the build() function in the code just peeks and pokes and updates all of the 24 pointers in a brute-force kind of style.

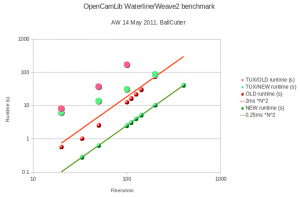
I suspect that the O(n^2) time-complexity is optimal, since with n X-fibers and n Y-fibers there will be roughly n*ninternal vertices in the grid, and they all have to be processed (?unless we can prune the grid and ignore internal areas and focus on the edge of the weave?).

Faster Waterline

I've written a new Weave class for opencamlib which makes the waterline operation faster.

The first test-case is a single triangle, and we calculate a number of waterlines at different z-heights using a ball-cutter:

The second test-case is the Tux model where we calculate a single waterline at some z-height. Note how using the chosen ball-cutter at this particular height the waterline splits into two separate loops.

(the yellow line is a plain waterline and the red line is an adaptive Waterline, but that's not important here)

Here is the runtime data. The smaller symbols show results from the one-triangle test-case. The old algorithm(red data points and line) seems to be slower than O(N^2), with a pre-factor of about 2 milliseconds. The time data for the new algorithm (green) fits an O(N^2) line better and has an almost 10-fold faster pre-factor of around 0.25 ms.

The speedup for the Tux model (large symbols) is even greater. With the old algorithm the slope of the data points (pink) looks much worse than N^2 and runtimes quickly reach a minute or more. With the new algorithm (big light green symbols) the runtime stays under 100s even at 200 fibers/mm.

This speedup was achieved by building a weave which is a directed half-edge graph, instead of the old undirected graph. The old algorithm first used connected_components (time complexity O(V + E)) to split the weave into its connected components. For each component a planar embedding was then constructed (time complexity ??), and the toolpath loop extracted with planar_face_traversal (time complexity O(V+E)).

In the new Weave, each edge has a "next" pointer pointing to the next edge of the face. This means we can extract the toolpath loop by following the "next" pointer until we find the next CL-point. Effectively the planar embedding is now contained in the graph datastructure and does not have to be computed separately. This also saves work since we don't have to traverse faces which do not produce toolpaths. This new solution to the weave point-order problemdeserves its own post in the near future - stay tuned...

Waterline problem

I was trying to work on a new adaptive waterline feature, but ended up uncovering an old existing problem/bug with waterline. I think it has to be a problem in either building the weave from the fibers, or constructing the planar embedding of the weave.

The yellow waterline should obviously be a smooth loop around the outside of the weave (red/green fibers) and not a zigzag journey back and forth... 🙁

Update: this is better now:

Update2: here's a figure where new fibers (red and green) are inserted adaptively where the shape of the waterline changes most. There's something wrong with building the planar embedding for this weave, so no yellow adaptive waterline path yet...

Update3: some progress at last (fixed a bug in adaptive drop-cutter at the same time):

The weave point-order problem

When creating waterlines or 2D offsets using a "sampling" or "CL-point based" approach the result is a grid or weave such as that shown in black above. The black lines can in principle be unevenly spaced, and don't necessarily have to be aligned with the X/Y-axis. The desired output of the operation is shown in red/orage, i.e. a loop around/inside this weave/grid, which connects all the "loose ends" of the graph.

My first approach was to start at any CL-vertex and do a breadth_first_search from there to find the closest neighboring vertices. If there are many candidates equally close you then need to decide where to jump forward, and do the next breadth_first_search. This is not very efficient, since breadth_first_search runs a lot of times (you could stop the search at a depth or 5-6 to make it faster).

The other idea I had was some kind of 'surface tension', or edge removal/relaxation where you would start at an arbitrary point deep inside the black portion of the graph and work your way to the outside as far as possible to find the output. I haven't implemented this so I'm not sure if it will work.

What's the best/fastest way of finding the output? Comments ?!

Update: I am now solving this by first creating a planar embedding of the graph and then running planar_face_traversal with a visitor that records in which order the CL-points were visited. The initial results look good: