Tag: push-cutter

Opencamlib cutter shapes

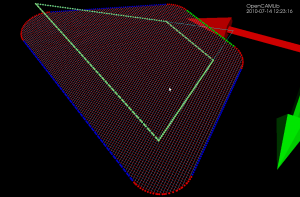
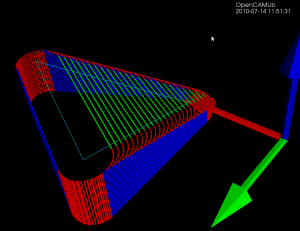
If you calculate toolpaths around a very narrow and 'pointy' triangle you will get toolpaths in the shape of the inverse cutter - the "Inverse Tool Offset". Here I've plotted the basic operations, in red/blue drop-cutter which drops the cutter down along the z-axis until it contacts the triangle, and in cyan waterlines which are the results of a push-cutter operation that pushes the cutter at constant z-height along the x/y axis into contact with the triangle.

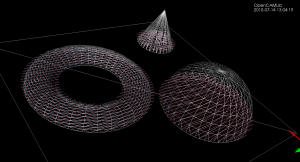
There are four basic cutter shapes: (1) Cylinder, (2) Sphere('Ball'), (3) Toroid('Bull'), and (4) Cone. The triangle contact can be divided into tests for contact with (a) the three vertices of the triangle, (b) the facet of the triangle, and (c) the three edges of the triangle. That's 4x3 = 12 contact/collision-test functions that have to be written (a few, particularly the facet-tests, can be combined into one base-class method).

Once the basic cutter shapes work it is possible to combine them through CompositeCutter. The bottom row shows cutters with a central part corresponding to the top row of cutters, and a conical outer part.

The point of this exercise is of course not only to plot inverse-tool-shapes, but to be able to calculate toolpaths for these and other CompositeCutter tool shapes. This will become more interesting if/when the cutting-simulation starts working and it will be possible to compare for example surface-finish vs. cutting-time of a BallCutter operation vs. a BullCutter operation.

Waterline toolpath experiment

The logical next step from drop-cutter ("axial tool projection" or "z-projection machining") is to instead push the cutter sideways("radial tool projection") against the model and get waterline (or "z-slice") paths. In addition to waterline finish-paths these paths can be used in roughing where they define pockets for 2D machining/clearing of stock. The general purpose tool-location function would be a non-axial tool projection, but I'm not going there unless someone sends me a state of the art 5-axis VMC as a present!

Push-cutter is different from drop-cutter, because in drop-cutter for 3-axis machining there is always only one right answer. There's one z-height where the cutter is positioned as low as possible, but doesn't interfere with the model. In drop-cutter positioning the tool above this z-height is OK, but dropping it further down is an illegal move which causes overcutting.

In push-cutter we push the cutter along a line (called a "fiber") in the xy-plane, and search for CL-points where the cutter touches a triangle, together with illegal points or stretches/intervals along the fiber where the cutter interferes. There are going to be many of these points and intervals, so the fiber needs to keep track of everything using a list of interfering intervals (the endpoints of the intervals are valid CL-points).
Similarly to drop-cutter, where a path is sampled along points in the (x, y) plane, we now need to build up our waterline-path by inserting closely spaced fibers in the x-direction and the y-direction. Eventually the CL-points start to form a continuous waterline, if we hook up the points into a list in the correct order. The x- and y-fibers form a grid (or mesh/weave), a kind of graph, which can be used to figure out the correct ordering of the CL-points (not implemented yet, see BGL).

This picture shows the original triangle (thin cyan lines), X-fibers (red lines), Y-fibers (blue lines), and the endpoints of the fibers, which are CL-points (colored by which element of the triangle they are hitting: red=vertex, green=facet, blue=edge). The light-green points are CC-points, i.e. points where the cutter makes contact with the triangle. This initial experiment uses a cylindrical cutter, and I expect the spherical cutter to follow soon, while the toroid will be more difficult...
weave

This picture does not show the fibers/weave, only CL-points, calculated at many different z-heights.
waterline_experiment

If the low-level functions are written right these ideas extend easily from the one-triangle test and debugging case to the practically more important and interesting many-triangle case: (note how now the weave-graph has three disconnected components)

demo_stl_waterline

Coming to an open-source CAM-system near you this summer/fall...