Tag: histogram

Photon-correlation test with modulated LED

Further testing of the time-stamping hardware. The idea was to generate a weak beam of light with an intensity modulation at 1-12 MHz, count and time-stamp the photons, and see if the modulation can be measured with a correlation histogram.

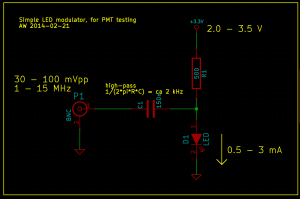
To generate a stream of photons intensity modulated at a frequency f_mod I used this simple LED circuit driven by an adjustable DC power-supply and a signal generator. I didn't test the bandwidth of the circuit and LED, but it seems to work well for this test at least up to 12 MHz.

led_modulator_2014-02-21

If we are given such a stream of photons, with an average rate of say 10 kphotons/s, how do we detect that the modulation at MHz frequencies is there? Note that the average rate of photons is much much smaller than the modulation frequency. If we receive photons at 10 kcounts/s there is on average 1000 cycles of modulation between each photon-event, when f_mod=10 MHz.

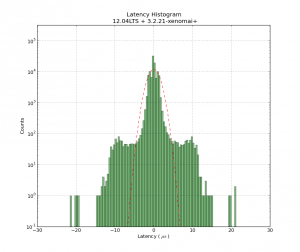
One way is to count the photons with a photon-counter, and time-stamp each photon. We should now on average see more/less photons every 1/f_mod seconds. So if we histogram all time stamps modulo 1/f_mod, we should get a sine-shaped histogram. This assumes that the signal generator creating f_mod and our time-stamping hardware share a common time-base.

This works quite nicely!

At the start of the video we see only the dark counts of the PMT. A DC voltage is then applied to the LED and the histogram rises up, but remains flat. When the modulation is applied we immediately see a sine-shape of the histogram. If we adjust the the frequency, phase, or amplitude of the modulation we see a corresponding change in the histogram.

The video first has testing at f_mod=1 MHz, with a histogram modulo 1/f_mod = 1000 ns, and later with f_mod=12 MHz and the histogram modulo 83333 ps. The later part of the video also has a least-squares sin() fit to the data.

This technique is very sensitive to mismatch between the applied frequency f_mod, and the histogram mod-time 1/f_mod. I first wanted to try this at 12 MHz, so I set the histogram mod-time to 83333 ps - and saw no sine-histogram at all! This was because I had rounded 1/f_mod to the nearest picosecond, and 1/83333 ps is actually 12 000 048 Hz - not 12 MHz!
At 12 MHz a deviation of 48 Hz is a few ppm in fractional frequency, and I later tested that changing f_mod by a fraction of ca 1e-8 makes the histogram slowly wander to the left or right. Any larger deviation and the correlation is lost.
All of this is similar to a lock-in technique, so the same principles should apply.

Latency Histogram

This shows a latency-histogram for a 1 ms thread running on Xenomai on my recently acquired ITX-board. Note how badly the histogram is approximated by a normal distribution (Gaussians look like parabolas with logarithmic y-scale!). See also Michael's recent RPi data and  Kent's Athlon/P4 data.

The usual latency-test numbers people report is the maximum latency, a measure of how far out to the left or right the most distant single data point lies. The histrogram can probably be used to extract many more numbers, but for real-time critical applications like cnc-machine control the maximum latency is probably an OK figure of merit.

The latency numbers are recorded with a simple HAL component:lhisto.comp

The instantaneous latency-number is then put in a FIFO by the real-time component sampler and written to a text-file using halsampler. I'm setting this up with the following HAL commands (put this in a file myfile.halrun and run with "halrun -f myfile.halrun")

loadrt threads name1=servo period1=1000000
loadrt sampler depth=1000 cfg=S
loadrt lhisto names=shisto
addf shisto servo
addf sampler.0 servo
net latency shisto.latency sampler.0.pin.0
start
loadusr halsampler -c 0  latencysamples.txt

The numbers can now be plotted with matplotlib. I'm using the following script:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab
# load data from file
x = np.loadtxt('latencysamples.txt' )
x=x/1e3 # convert to microseconds
 
fig = plt.figure()
ax = fig.add_subplot(111)
nbins = len(x)/1000
n, bins, patches = ax.hist(x, nbins,  facecolor='green', alpha=0.5, log=True)
bincenters = 0.5*(bins[1:]+bins[:-1]) # from matlplotlib example code
mu = np.mean(x)
sigma = np.std(x)
area = np.trapz(n,bincenters) # scale normpdf to have the same area as the dataset
y = area * mlab.normpdf( bincenters, mu, sigma)
l =  ax.plot(bincenters, y, 'r--', linewidth=1)# add a 'best fit' line for the normal PDF
 
ax.set_xlabel('Latency ( $ \mathrm{ \mu s } $ ) ')
ax.set_ylabel('Counts')
ax.set_title('Latency Histogram\n 12.04LTS + 3.2.21-xenomai+')
ax.set_ylim(1e-1, 10*max(n))
ax.grid(True)
plt.show()