Tag: code

Arc predicates

I started working on arc-sites for OpenVoronoi. The first things required are an in_region(p) predicate and an apex_point(p) function. It is best to rapidly try out and visualize things in python/VTK first, before committing to slower coding and design in c++.

in_region(p) returns true if point p is inside the cone-of-influence of the arc site. Here the arc is defined by its start-point p1, end-point p2, center c, and a direction flag cw for indicating cw or ccw direction. This code will only work for arcs smaller than 180 degrees.

def arc_in_region(p1,p2,c,cw,p):
    if cw:
        return p.is_right(c,p1) and (not p.is_right(c,p2))
    else:
        return (not p.is_right(c,p1)) and p.is_right(c,p2)


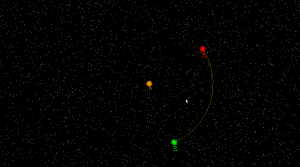
Here randomly chosen points are shown green if they are in-region and pink if they are not.

apex_point(p) returns the closest point to p on the arc. When p is not in the cone-of-influence either the start- or end-point of the arc is returned. This is useful in OpenVoronoi for calculating the minimum distance from p to any point on the arc-site, since this is given by (p-apex_point(p)).norm().

def closer_endpoint(p1,p2,p):
    if (p1-p).norm() < (p2-p).norm():
        return p1
    else:
        return p2
 
def projection_point(p1,p2,c1,cw,p):
    if p==c1:
        return p1
    else:
        n = (p-c1)
        n.normalize()
        return c1 + (p1-c1).norm()*n
 
def apex_point(p1,p2,c1,cw,p):
    if arc_in_region(p1,p2,c1,cw,p):
        return projection_point(p1,p2,c1,cw,p)
    else:
        return closer_endpoint(p1,p2,p)


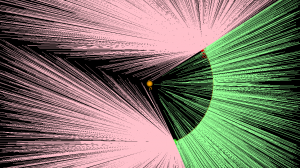
Here a line from a randomly chosen point p to its apex_point(p) has been drawn. Either the start- or end-point of the arc is the closest point to out-of-region points (pink), while a radially projected point on the arc-site is closest to in-region points (green).

The next thing required are working edge-parametrizations for the new type of voronoi-edges that will occur when we have arc-sites (arc/point, arc/line, and arc/arc).

Uniform random points in a circle using polar coordinates

I need this seldom enough to forget how it's done - but then it's annoying to have to think/google for the solution again when I do need it... So I'll document here.

The task is to generate uniformly distributed numbers within a circle of radius R in the (x,y) plane. At first polar coordinates seems like a great idea, and the naive solution is to pick a radius r uniformly distributed in [0, R], and then an angle theta uniformly distributed in [0, 2pi]. BUT, you end up with an exess of points near the origin (0, 0)!  This is wrong because if we look at a certain angle interval, say [theta, theta+dtheta], there needs to be more points generated further out (at large r), than close to zero. The radius must not be picked from a uniform distribution, but one that goes as

pdf_r = (2/R^2)*r

That's easy enough to do by calculating the inverse of the cumulative distribution, and we get for r:

r = R*sqrt( rand() )

where rand() is a uniform random number in [0, 1]. Here is a picture:

fig2

some matlab code here.

The thinking for generating random points on the surface of a sphere in 3D is very similar. If I get inspired I will do a post on that later, meanwhile you can go read these lecture notes.