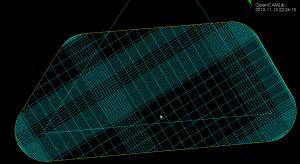
Previously the flat() predicate looked only at the number of intervals contained in a fiber when deciding where to insert new fibers in the adaptive waterline algorithm. Here I've borrowed the same flat() function used in adaptive drop-cutter which computes the angle between subsequent line-segments(yellow), and inserts a new fiber(cyan) if the angle exceeds some pre-set threshold.
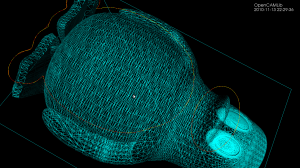
This works on the larger Tux model also. However, there's no free lunch: the uniformly sampled waterline (yellow) runs in about 2 s (using OpenMP on a dual-core machine), while the adaptively sampled waterline takes around 30s to compute (no OpenMP).
The difference between the adaptive (red) and the uniformly sampled (yellow) waterlines is really only visible when zooming in on sharp corners or other details. Compare this to adaptive drop-cutter.


Hi Anders,
Provided your input data is a triangular mesh ... won't be more accurate and simpler to just slice the mesh with a vertical plane matching the machining line of the zigzag and using the points obtained instead of samples?
Cheers,
misan
Hi again,
Well, the above was meant as a replacement to adaptive sampling for parallel finishing using dropcutter. But after testing my idea I can see that sampling is definitely faster than what I suggested.
Hi,
In some special cases you might be able to reduce the 3D collision (cutter against STL model) to a 2D problem. However in the general case this is really a 3D problem since we don't know that the cutter-contact (CC) point will be exactly on the 'drive-plane' where we have the cutter-location (CL) point.
This holds for both drop-cutter and for waterline. They are really 3D problems unless you restrict to some special geometries. For example if you have only cylindrical cutters and you have models without undercuts ('inward' bending geometry) then it might be possible to simplify.