Month: January 2012

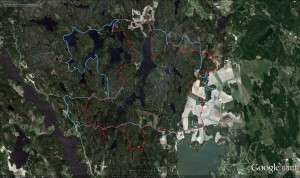
8h Rogaining, Espoo

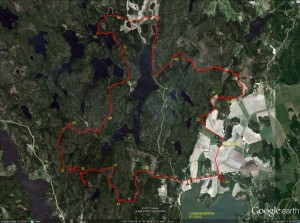
Took part in an 8h rogaining event yesterday. Very wet in the forest with a lot of fallen trees due to the storms over the last few weeks.

We planned a ca. 20km long route (straight lines between controls), assuming we would walk up to 50% more, i.e. around 30km, which would be OK for 8 hours.

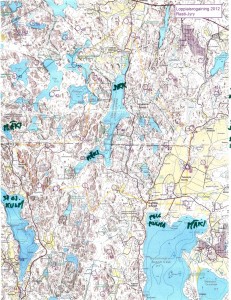
This event had a 1:25000 map which was much easier to read compared to the 1:40000 one last fall. No problems in the beginning, we fould 23 -> 21 -> 31 -> 41 quite easily. The first digit of the control-numnber indicates how many points you get for the control. The next control 51 was worth five points, and they are usually harder to find. Not this time, since it was at the very top of a hill, and people before us had already left tracks in the snow.

Then comes the big mistake of the day. We follow another faster group west down the hill from 51 towards 32. For some inexplicable reason we then completely mis-place ourselves on the map and although we are practically within reach of 32 we make a slow detour south before we realize where we are. Update: I have since learned that our confusion most probably was caused by a brand new road in this area, which was not marked on the map!

Probably annoyed by the first mistake, the second mistake of the day comes on the very next control: between 32 and 37 we take the wrong path north-east and decide to head back when we realize that.

So far we had stuck to the plan, but looking at the watch at 37 we decided to cut 39 from the route. Walk north along the road to 26, and then more walking along a big and then a small road to 57. At 57 we had some discussion about whether to walk back along the road, or try to find the electric lines north of 57 and let them guide us to the road. We had used 4 hours, or half of the total time here. We chose the latter route, and a straight northward pointing bit of our path after 57 indicates where we walked under the electric lines. Close to 53 the plan was to follow a path to the right of the hill and then the ditch to the control. Things didn't go to plan and we ended up to the left of the hill, but found the control with the help of tracks in the snow and voices/lights of others. A walk along the lake-shore to 55. And further north to a road.

So far we had roughly followed the plan. But now we had less than 3 hours left, and it was already dark making orienteering in the woods without clear paths or roads much harder. We decided to forget the plan and walk mostly along roads towards the finish, taking controls close to roads/paths along the way. A long bit of walking first south and then northeast to 49. Another long bit of walking all the way to 24. Here the image shows double GPS-paths because I switched from the 405cx watch to the Edge800 I use on the bike. We still had 45-50 minutes left at 24, so with a close eye on the clock we find 33 quite easily and 22 with a little more effort. We finished with about 12 minutes to spare.

About 90 teams (either solo, or in teams of 2-4 persons) took part.

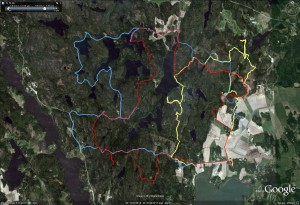
Update, here's our route again (in red), compared to another slightly faster team's route in blue:

Update 2: map with tracks from three teams:

TTT++ and font-vd

Update: Now all the capital letters work!

I wanted to test my VD algorithm on font-outlines. So I ported Chris Radek's truetype-tracer to c++ and added some python bindings. Here: https://github.com/aewallin/truetype-tracer

Because my VD code cannot handle circular arcs yet, I took some old code from TTT 3.0 and made converting conics and cubics, the native output of FreeType, as well as arcs into line-segments optional.

Predictably, OpenVoronoi crashes in many cases, but here is an "L" that works:

VD for polylines and polygons

I've been hacking away at openvoronoi, adding support for polylines and polygons.

The code I had in November works with individual non-intersecting line segments, like this:

Note how each vertex in the figure above is of degree three, i.e. there are three edges incident on each vertex. There's something about the number three, or triangles, or both, that makes planar graphs of degree three particularly nice to work with.

Here's the same figure with some notes describing the elements. The line-sites are drawn in yellow, and are associated with their left R(L+) and right R(L-) regions. The purple lines are called separators, and they define the region associated with the start- or end-point of a line-site. The three possible edge-types are also shown: LineEdge between two point-sites, LineEdge between two line-sites, and a Parabolic (PointLine) edge between a point-site and a line-site.

Now, things get more complicated when we want to 'glue' two line-segments end-to-end in a polyline, or glue three or more line-segments together to form a polygon. Vertices are not necessarily of degree three any more. In fact the vertex degree is essentially unbounded, as you can start/end arbitrarily many line-segments at the same vertex. The solution I am using is to introduce what I call a null-face with zero-length null-edges around each point-site to which more than one line-segment connects. The mental picture is much like that of a key-chain, or mountaineering carabiners that are hooked-in to a loop. When we want to use the a vertex as a start/end-point for a segment we 'hook-in' to the null-face:

This introduces a number of new rules and associated code for how vertices should be created, removed, and moved around a null-face, but it seems to work somehow now:

Note how these null-faces and the circular null-edges around each end-point result in degree three vertices, which are much nicer to deal with in the algorithm. For example, the null-face around vertex "0" is 40->85->86->41->39. Without the null-face construction this vertex would be of degree five. Here is an annotated version of the same picture:

This image shows how the diagram divides the plane into regions associated with endpoints such as R(0) and with the right/left side of a line-segment such as R(0-29) and R(29-0). The null-edges that form null-faces around each end-point are drawn in white.

Of course, these null-edges are only a topological construction. Geometrically we can position each vertex on a null-face at the location of the encircled point-site. This effectively contracts away the zero-area null-faces, and the result is the diagram we want:

The code now runs for a few select test-cases. To be continued...

Update: The code now seems to work also for random polygons with a large number of vertices. Here is one with 400 vertices:

and 3200-vertices: